Sub-optimal Block Matching Algorithms (part 2 of 2)
There are a number of sub-optimal block matching algorithms that use the quadrant monotonic assumption.Detailed descriptions of are available for the following BMAs:
- 2-D Logarithmic Search (TDL) Jain&Jain
- Three Step Search (TSS) Koga
- Orthogonal Search Algorithm (OSA) Puri
- One at a Time Search (OTS)
- Cross Search Algorithm (CSA)
- Greedy Algorithms Manning
A comparison of the effectiveness of these algorithms under different circumstances is available from the Experiments & Conslusions section.
Dynamic Search Window Algorithm
The Dynamic Search Window Algorithm (DSWA) attempts to achieve improved performance by directly addressing the problem of convergence on local minima [Lee93]. Although this algorithm starts with a step size in the normal way, the extent to which the area of the search window decreases depends on the difference between the minimum distortion and the second lowest distortion. Lee et al. used three convergence modes : fast, normal, and slow. If the difference between the two lowest distortions was small then the outcome of a stage of the algorithm was deemed inconclusive and so the step size was reduced only a little (slow). This gave the algorithm the opportunity to recover if, in fact, the wrong point was chosen. Conversely, if the difference between the two lowest distortions was large, then the algorithm converged more quickly on the minimum (fast). If the difference between the two lowest distortions fell between the thresholds for fast and slow modes then the algorithm reduced the search area in the normal way.Lee et al tested dynamic search windows with an alternating saltire (+) and Greek (x) cross pattern, with the step size multiplied by 1/4, 1/2, and 3/4, in fast, normal, and slow modes respectively. They found that this algorithm used fewer computations but produced better results than the Three Step Search under similar circumstances.
Dependent Algorithms
The are two primary sources of motion in image sequences. They are camera motion (zoom, pan, and tilt) and the motion of objects within the scene. Since blocks are generally smaller than the objects it is reasonable to assume that there is correlation between the motion of adjacent blocks [DeWi92]. Dependent block matching algorithms calculate the motion of a given block with the aid of the motion vectors of its neighbouring blocks. The motion vectors of the neighbouring blocks are used to calculate a prediction of the block's motion and this prediction is used as a starting point for the search. Dependency introduces memory into the block matching algorithm, but usually results in a more ordered set of motion vectors.Dependency can be spatial or temporal or both.
Spatial Dependency
Spatial dependency exploits the correlation between the motion vectors of neighbouring blocks to provide a prediction to matching algorithms as to the likely position of a block's match. Frequently the prediction is formed by taking a weighted average of the neighbouring blocks' motion vectors. Because exploiting spatial dependency can help find better matches and find matches more quickly, a number of researchers have suggested schemes that use spatial dependency to assist block matching algorithms [Jang91] [Reut89] [Stil90].
Predictions for block matching algorithms can be derived from the motion of some of its neighbours. A typical block has eight immediate neighbours. Depending on the order in which target blocks are matched (typically top-to-bottom and left-to-right), the motion vectors for some of these neighbours might not be available when a block is being matched.
The order in which blocks are matched restricts the choice of neighbouring blocks that can be used. If the candidate blocks are matched in a left-to-right and top-to-bottom order, then three neighbours will be available to assist matching, as in Figure a. Alternatively only two of these three might be used as in Figure b. An even simpler scheme might use just the motion vector of the block immediately to the left of the target block to assist the matching algorithm, as in Figure c. Using only motion vectors from blocks to the left or above a candidate block can cause problems at object boundaries. Thus it might be desirable to use the motion vectors of the neighbouring blocks above, below, and to the left and right of the target block, as in Figure d. This can be achieved by carefully considering the order in which candidate blocks are matched.
a b c d e
Examples of spatial dependency patterns. Dark boxes indicate target block and lighter boxes represent the neighbours whose motion vectors assist the matching algorithm.

Dependency pattern for a three-pass matching algorithm exploiting spatial dependency. Matches are found for candidate blocks illustrated in red, followed by those in orange, and lastly yellow.
The above diagram illustrates a multi-pass process where initially a match is found for only every second block of every second row. During the next pass every second block of every other row is matched using the motion vectors of the neighbouring blocks at each of its corners (See Figure e). Finally the remaining half of the blocks are matched using the neighbours at their sides as in Figure d.
To circumvent the problems associated with spatial dependency at object boundaries, some spatially dependent algorithms do not average the neighbouring vectors. Instead they consider how many of the neighbouring vectors are similar. If, for example, the motion vectors of four neighbouring blocks are considered and the motion vectors of three of these are the same, then the motion vector similar to theirs might be chosen as a starting position for the search. If the motion vectors of the neighbouring blocks are not sufficiently uniform then the search for the target block might be carried out as normal, as though no spatial dependency was being exploited.
Temporal Dependency
If the assumption is made that moving objects in a scene move with constant velocity then a large degree of temporal redundancy can be expected. This redundancy can be exploited in a manner similar to spatial redundancy by providing predictions to block matching algorithms as to likely positions of matching blocks. By examining the motion of blocks in the previous frame(s), predictions about their behaviour in the current frame can be made.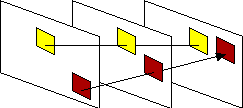
The distance and direction of object motion between frames tends to remain the same from frame to frame. Temporal redundancy exploits this tendncy by assuming that motion vectors from previous frames indicate good starting points for searches in subsequent frames.
Ninomiya and Ohtsuka implemented a temporally dependent system that took into account the motion vector of the block at the same position in the previous frame [Bowl85]. Puri et al devised a temporally dependent variation of the orthogonal search algorithm that also examined the motion vector of the same position in the previous frame. They found that the temporal dependency allowed the algorithm to achieve results similar to the independent variation but required fewer searches [Puri87].
Both spatial and temporal dependency can be exploited simultaneously [Hsie90].
The kinds of block matching algorithms used on this page are frequently used when coding MPEG. There are however more advanced block matching techniques that are also very interesting. They are not suitable for use with MPEG however.
Ninomiya and Ohtsuka implemented a temporally dependent system that took into account the motion vector of the block at the same position in the previous frame [Bowl85]. Puri et al devised a temporally dependent variation of the orthogonal search algorithm that also examined the motion vector of the same position in the previous frame. They found that the temporal dependency allowed the algorithm to achieve results similar to the independent variation but required fewer searches [Puri87].
Both spatial and temporal dependency can be exploited simultaneously [Hsie90].
The kinds of block matching algorithms used on this page are frequently used when coding MPEG. There are however more advanced block matching techniques that are also very interesting. They are not suitable for use with MPEG however.