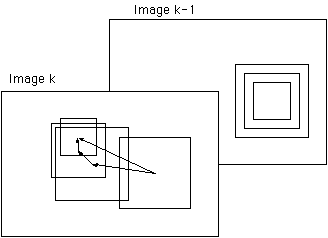
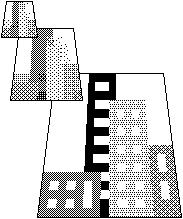
A three level hierarchical search. Initially large blocks are matched and the resulting motion vector provides a starting point for a search for a smaller matching block. Taken from [
Bier88]
Bierling developed a hierarchical block matching algorithm that started by matching a large target block with a similar sized block in the past frame. The resulting motion vector is then used as an estimate for a search using smaller target and candidate blocks [Bier88]. At each stage the resulting estimate was used as a starting point for the next stage of the search, as illustrated above. The size of the block was reduced and a match found at each stage of the algorithm, until the matching blocks were the desired size.
It is easy to see how this algorithm might match true motion more easily than those that use only small blocks. But the algorithm is very computation intensive. This computational burden can be eased by modifying the algorithm in three ways.
In the early stages, when the target blocks are largest, the candidate motion vectors could be coarse. That is, only a subset of the possible motion vectors in the search space need be considered, as in Gilge’s algorithm. Although, the initial estimates might not be ideal, the algorithm would have the necessary flexibility in later stages to make up for this.
In addition, the matching criteria could use only a sub-sample of the pixels in the large blocks, thus reducing the number of pixels that need to be compared. For example, only pixels from every second row and column from both the target and candidate blocks might be compared. It is unlikely that such a modification would adversely affect the performance of the algorithm but it would preserve the advantages of using large blocks at the early stages.
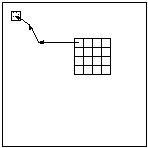
A third modification could allow Bierling's algorithm to make better use of the information gathered during each stage. If the size of the blocks for each stage was chosen such that several smaller blocks could fit into one large block, then the approximation generated at one stage can be applied to several blocks during the subsequent stage, instead of just one. (llustrated below)
Progressive refinement of a motion vector. The motion vector for each block is applied to four corresponding blocks in the layer below.
Combining all three modifications results in a more popular block matching technique that uses image pyramids and block decomposition. Each frame of an image sequence is stored in pyramid form. There are a number of pyramid coding techniques for example those of
[
Wang92]
[
Sefe92]
[
Chen88]. They all store images in multiple layers such that each pixel in an upper layer contains information about several pixels in the layer below.
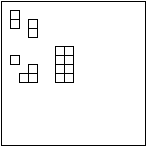
In the figure above each pixel in the upper layers has a value that is the average of the corresponding 2x2 block of pixels in the layer below. In a scheme that uses image pyramids, blocks from the low resolution layers of the past and current frame are matched using a simple block matching algorithm (for example an exhaustive search). The resulting motion vectors are then used as starting points for matching algorithms in the next layer. Hierarchical algorithms are similar to spatially and temporally dependent searches, except that the predictions do not come from the current or previously coded frame, but from matches that have taken place on a lower resolution version of the current frame. In the case of Figure 4.3 each motion vector provides start points for searches for four target blocks.
Wang & Clarke found that their hierarchical encoding technique performed better than conventional methods [
Wang92]. Seferidis & Ghanbari developed a three level hierarchical system [
Sefe92]. They found that one of the main problems with such systems was that they had difficulty overcoming mistakes made in the early stages. A great many researchers are investigating hierarchical coding techniques because of their reliability and the quality of the matches they produce. Hierarchical coding schemes are of course considerably more complex than confessional video coding techniques.
[return to
Advanced BMAs]
© Colin E. Manning 1996