Sub-optimal Block Matching Algorithms
The exhaustive search is computationally very intensive and requires the distortion function to be evaluated many times for each target block to be matched. Considerable research has gone into developing block matching algorithms that find suitable matches for target blocks but require fewer evaluations. Such algorithms test only some of the candidate blocks from the search area and choose a match from this subset of blocks. Hence they are known as sub-optimal algorithms. Because they do not examine all of the candidate blocks, the choice of matching block might not be as good as that chosen by an exhaustive search. The quality-cost trade-off is usually worthwhile however.
Signature Based Algorithms
Signature based algorithms successfully reduce the complexity of block matching while preserving many of the advantages of the exhaustive search. Signature based algorithms reduce the number of operations required to find a matching block by performing the search in a number of stages using several matching criteria. During the first stage every candidate block in the search area is evaluated using a computationally simple matching criteria (e.g. pel difference classification). Only the most promising candidate blocks are examined during the second stage when they are evaluated by a more selective matching criteria. Signature based algorithms may have several stages and as many different matching criteria.
Khakoo tested signature based algorithms using a two phase process where some of the coefficients of a DCT performed on the target and candidate blocks were used as the signature function and the MAD criterion was used at the final stage [Khak89]. The results of his experiments showed that signature based algorithms can produce higher quality images than some other sub-optimal algorithms (discussed later in this section), but at the expense of greater computational complexity. Ahmad Fadzil and Dennis used a technique known as phase correlation as a signature function to suggest five candidate blocks which were then evaluated using the MSD criterion [
Ahma90]. Chan et al. used the Pel Difference Classification (PDC) criteria with a high threshold during the first stage of their algorithm. The threshold was then halved at each stage until only a few candidate blocks remained [
Chan94].
Coarse quantization of vectors
While signature based algorithms reduce complexity by minimising the complexity of the criteria applied to each block in the search space, the remainder of the block matching algorithms discussed in this chapter reduce complexity by reducing the number of blocks to which the criterion is applied. These algorithms consider only a subset of the search space.
The decision on which candidate blocks to examine and which candidate blocks to ignore is never arbitrary. Various sub-optimal block matching algorithms are based on different assumptions about the image data they are compressing and based on these assumptions employ strategies that suggest which candidate blocks should be examined at a given stage.
The first such assumption is about the viewer rather than the data itself. Research indicates that humans cannot perceive fast moving objects with full resolution, which results in fast moving objects appearing blurred [
Bowl85]. Thus if the quality of an image portion containing a fast moving object was to drop whilst the object was in motion, this reduction in quality might go unnoticed.
With this characteristic in mind Gilge suggested a search pattern to be used in place of the full search [
Gilg88]. All candidate blocks close to the centre of the search area (i.e. around the zero vector) are evaluated as potential matches, but only a subset of the candidate blocks far from the centre are considered. This results in slow moving or stationary objects being coded with the best available match, whereas fast moving blocks might be coded with less ideal matches. The figure below illustrates the search pattern that could be used in place of a full search with a maximum displacement of ±6 pixels in both the horizontal and vertical directions. For a search area of this size the number of matching criteria evaluations is reduced from 169 to 65.
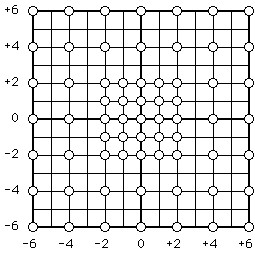
Figure 3.3 Search pattern for a matching algorithm that coarsely quantizes motion vectors of fast moving objects. Adapted from [
Gilg88]
Principle of Locality
The principle of locality suggests that very good matches, if they exist, are likely to be found in the neighbourhood of other good matches. For example, the assertion that "if the wine from a particular winery is very good then the wine from a nearby winery is likely to be good" is based on the principle of locality. Although such assumptions can prove false, they are nonetheless useful. Block matching algorithms that are based on the principle of locality first examine a sparsely spaced subset of the search area and then narrow the search to only those areas that show promise.
One of the simplest applications of the principle of locality to the block matching problem is the two level hierarchical search described by Jaureguizar, Rhonda, and García [
Jaur92]. This algorithm initially examines a number of sparsely spaced candidate blocks from the search area and chooses the best match from these to be the centre of a finer search. This algorithm is illustrated in Figure 3.4 with maximum displacements of 5 pixels and 10 pixels in the vertical and horizontal directions respectively.
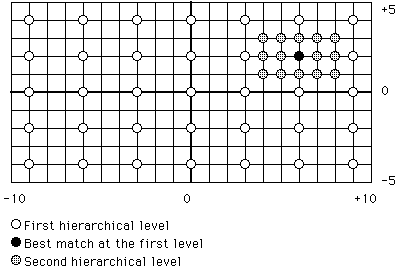
Figure 3.4 Two-level hierarchical search. Taken from [
Jaur92]
Returning to the quest for the finest winery, it is easy to see how a hierarchical algorithm could have multiple levels. The illustration below shows how the principle of locality could be used in conjunction with a hierarchical algorithm to make the search for the best winery cheaper by requiring fewer wines to be tasted. This illustrates a three level algorithm.
Gilge developed a second algorithm which has several stages. The first stage is similar to his earlier algorithm with candidate blocks that are far from the centre more sparsely spaced. Once the best match from these is found, however, its position becomes the centre of a denser search [
Gilg88].
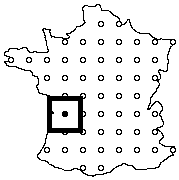
First hierarchical level - Second hierarchical level

Third hierarchical level

Best match at first level

Best match at second level

Best match at final level
Example of a three level hierarchical search based on the principle of locality.
Quadrant monotonic
By adopting a
quadrant monotonic model of the image data to be compressed, it is possible to significantly decrease the number of computations required to find a matching block, without significantly decreasing the suitability of the match [
Jain81]. The quadrant monotonic model, first used for block matching by Jain & Jain, assumes that the value of the distortion function increases as the distance from the point of minimum distortion increases. Therefore, not only are candidate blocks close to the optimal block better matches than those far from it, but the value of the distortion function is a function of the distance from the optimal position. Thus the quadrant monotonic assumption is a special case of the principle of locality. The strength of a radio signal at various distances from the transmitter is an example of quadrant monotonic data. The quadrant monotonic model was so applicable that a Honolulu radio station routinely transmitted all night in order to guide aircraft travelling from the mainland [
Stew95]. This practice inadvertently assisted the Japanese in finding their target in 1941. At the begining of the war BBC television ceased transmission in order to protect London.
The quadrant monotonic assumption allows for the development of sub-optimal algorithms that, like others, examine only some of the candidate blocks in the search area. In addition they use the values of the distortion function to guide the search towards a good match. Because not all of the candidate blocks are examined, the match found might not be the best available. But the trade-off between the quality of the match and the number of matching criteria evaluations is usually good.
The quadrant monotonic assumption does not a valid assumption.
Local minima can throw block matching algorithms off course.
[Sub-optimal block matching algorithms
part 2]
© Colin E. Manning 1996 Main Digital Video Page




