The problem of local minima
If the search area is so large that the quadrant monotonic model does not apply to the entire search area then the algorithm might converge on a local minimum. A local minimum is a candidate block location where the neighbouring blocks have greater distortion but the candidate block is not the best of the entire search area. Thus the block is only the best within its own locality and a better block is available elsewhere in the search area.
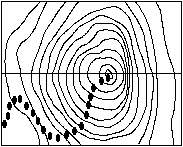
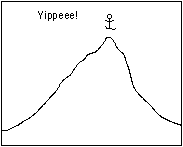
Mountain climber using the quadrant monotonic assumption to reach the peak. On the left is a contour map where the quadrant monotonic assumption holds over the entire search area with the corresponding profile on the right. The climber succeeds in finding the peak because the assumption holds.
The quadrant monotonic assumption and the problem of local minima are analogous to a mountain climber making the assumption that from an arbitrary starting position he will eventually arrive at the highest point as long as he continues to climb up (Illustrated above). This is of course true if there is only one peak. If there is more than one peak, however, the climber might arrive at a point where moving in any direction results in a drop in altitude and mistakenly conclude that he has reached the highest peak in the range. (Illustrated below).
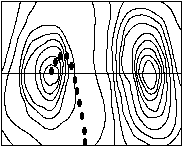
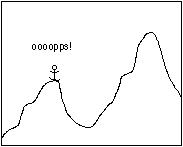
In this illustration the mountain climber again uses the quadrant monotonic assumption to reach the peak. On the left is the contour map showing that the quadrant monotonic assumption does not hold over the entire search area. The climber fails because the quadrant monotonic assumption does not hold.
Local minima are common in images and the local minima are typically not as good as the global minimum. This is a serious problem for sub-optimal block matching algorithms.
[Sub-optimal BMAs
part 1]
[Sub-optimal BMAs
part 2]
© Colin E. Manning 1996 Main Digital Video Page





